目的

对齐对风控时间序列预测项目的理解（从问题到解决方案），详细描述Transformer和Timer模型如何解决长距离时间依赖问题，以及在实际风控告警场景中的应用价值。

1. 项目背景与问题分析

1.1 当前告警机制的局限性

我们现在的告警方式：基于同比环比进行监控

  • 同比：和上个小时同期相比，交易量是否异常
  • 环比：和上一个周期相比，交易量是否异常

这种方式简单直接，但遇到一个问题：一旦出现时间相关的正常上涨，就会误报。

1.2 实际业务场景中的问题案例

案例1：中东月底发薪日

  • 中东地区每月月底发薪
  • 发薪后，用户充值行为会显著增加
  • 这是正常的、可预期的交易上涨

案例2：每月1号游戏首充资格刷新

  • 很多游戏在每月1号刷新首充奖励资格
  • 用户会在1号集中充值，获取首充奖励
  • 这也是时间相关的正常上涨

案例 3：活动

  • 一旦出现活动，因为和历史数据相比过高，所以会大批量告警

1.3 传统RNN模型的局限性

为了解决这个问题，我们考虑过使用RNN（循环神经网络）来学习时间序列模式。

RNN的工作原理：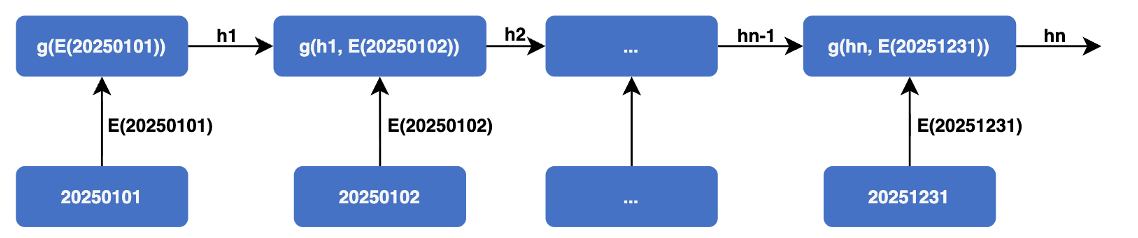
RNN工作原理

RNN的问题：

  • 信息衰减：随着时间步增加，早期信息会逐渐丢失
  • 梯度消失：训练时，梯度在反向传播过程中会越来越小
  • 无法并行：必须按顺序处理，速度慢

我们的需求:

  • 识别30天前的月底发薪日模式
  • 识别60天前的周期性充值模式
  • 理解”上个月1号充值上涨，这个月1号也会上涨”这种长期规律

1.4 解决方案

使用Transformer的注意力机制，让模型能够”同时看到”所有历史时间点，学习长距离依赖关系。

2. Transformer基本原理

2.1 从RNN到Transformer的演进

为什么需要Transformer？

想象一下，预测明天的天气，有两种方式：

方式1：RNN的方式（像人读文章）

  • 从第一天开始，一天一天地看
  • 看到第 60 天，基于前 59 天的情况去预测下一天，第一天的情况基本忘了

方式2：Transformer的方式（像人看地图）

  • 把 60 天的数据全部摊开，像看地图一样
  • 可以同时看到第1天、第10天、第30天、第60天
  • 可以自由地在不同时间点之间”跳转”和”关联”
  • 不会因为距离远就忘记

这就是Transformer的核心优势：并行处理 + 全局视野

怎么能知道哪天跟我关系最大呢？需要引入几个核心参数矩阵：

  • Query：当前时间点，我想预测什么？
  • Key：历史所有时间点，哪些时间点和我相关？
  • Value：相关时间点的实际数值
  • 注意力权重：每个历史时间点对当前预测的贡献程度

也就是说，有一个预处理过程：

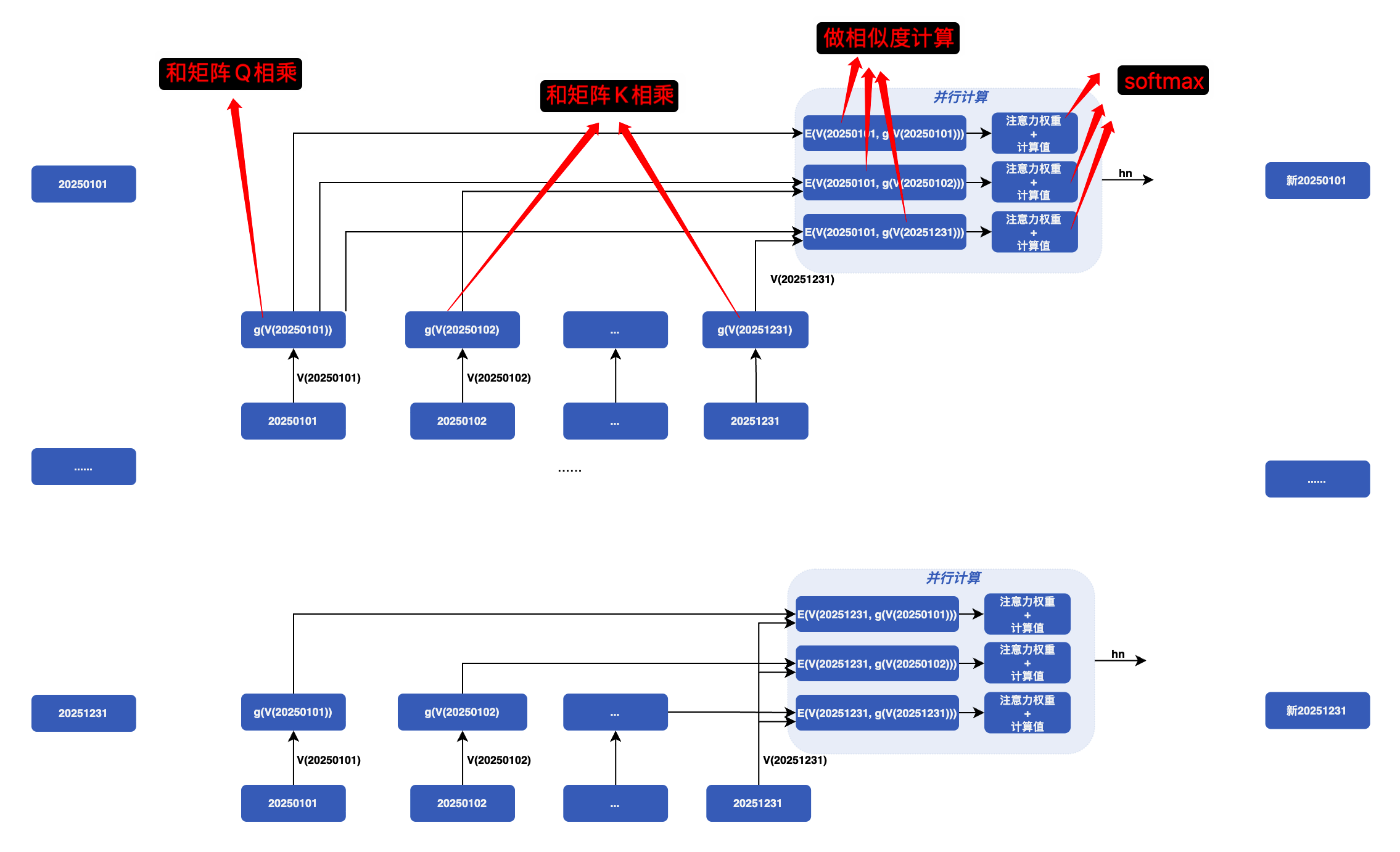
Transformer信息流

这里，将历史数据经过预处理，得到全新的历史数据，比如 20250101，经过处理之后得到了新的 20250101，这个 20250101 数据有这天和所有历史数据的相关性等信息。
并且这里的计算是全并行的。

2.2 Attention机制详解

在时间序列中，每个时间点都会：

  1. 计算自己和所有其他时间点的相似度
  2. 根据相似度，决定关注哪些时间点
  3. 用加权求和的方式，融合所有相关信息

具体过程：

graph LR
    A[输入序列
t1, t2, t3, ..., tn] --> B[计算Query, Key, Value]
    B --> C[计算相似度
Q × K^T]
    C --> D[Softmax归一化
得到注意力权重]
    D --> E[加权求和
权重 × Value]
    E --> F[输出
融合后的表示]

数学公式（简化理解）：

1
2
注意力权重 = softmax(Q × K^T / √d)
输出 = 注意力权重 × V

通俗解释：

  • Q × K^T：计算每个时间点之间的相似度（相似度越高，相关性越强）
  • softmax：把相似度转换成概率分布（所有权重加起来等于1）
  • 权重 × V：根据相关性，对历史数据进行加权求和

2.3 QKV机制的数学原理

QKV的数学定义

Query, Key, Value的本质：

在时间序列中，每个时间点的数据 x_i 通过三个不同的线性变换，得到三个不同的表示：

$$
Q_i = x_i W_Q, \quad K_i = x_i W_K, \quad V_i = x_i W_V
$$

其中：

  • $W_Q, W_K, W_V$ 是可学习的权重矩阵
  • $Q_i$（Query）：表示”我想了解什么”
  • $K_i$（Key）：表示”我能提供什么信息”
  • $V_i$（Value）：表示”我的实际内容”

为什么通过Q×K^T计算相似度？

点积的几何意义：

两个向量的点积可以表示它们的相似度：

$$
Q_i \cdot K_j = |Q_i| \cdot |K_j| \cdot \cos(\theta)
$$

其中 $\theta$ 是两个向量之间的夹角。

关键理解：

  • 如果 $Q_i$ 和 $K_j$ 方向相似（夹角小），点积大 → 相似度高
  • 如果 $Q_i$ 和 $K_j$ 方向相反（夹角大），点积小 → 相似度低
  • 如果 $Q_i$ 和 $K_j$ 垂直（夹角90°），点积为0 → 不相关

Softmax如何让参数拥有”注意力权重”的含义

Softmax的数学定义：

$$
\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}
$$

Softmax的关键性质：

  1. 归一化：所有输出值的和为1
    $$
    \sum_{i=1}^{n} \text{softmax}(z_i) = 1
    $$
    这使得输出可以解释为”概率分布”或”权重分配”

  2. 放大差异：Softmax会放大较大的值，抑制较小的值

    • 如果 $z_1 = 5, z_2 = 1$，则 $\text{softmax}(z_1) \approx 0.98$，$\text{softmax}(z_2) \approx 0.02$
    • 差异从 5:1 放大到 98:2

  3. 单调性：如果 $z_i > z_j$，则 $\text{softmax}(z_i) > \text{softmax}(z_j)$

在注意力机制中的应用：

$$
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q K^T}{\sqrt{d}}\right) V
$$

缩放因子 $\sqrt{d}$ 的作用：

  • 防止点积值过大，导致softmax梯度消失
  • 当 $d$ 很大时，$Q K^T$ 的值可能很大，softmax会变得很”尖锐”（只有一个值接近1，其他接近0）
  • 除以 $\sqrt{d}$ 可以稳定训练

数值示例：

假设计算得到的相似度分数为：$[2.0, 1.0, 0.5, 0.1]$

  1. 不缩放：$\text{softmax}([2.0, 1.0, 0.5, 0.1]) \approx [0.66, 0.24, 0.08, 0.02]$
  2. 缩放后（假设 $d=64$，$\sqrt{d}=8$）：$\text{softmax}([0.25, 0.125, 0.0625, 0.0125]) \approx [0.31, 0.28, 0.25, 0.16]$

缩放后的分布更平滑，有利于学习。

为什么加权求和能融合信息？

加权求和的数学表示：

$$
\text{Output}i = \sum{j=1}^{n} \alpha_{ij} V_j
$$

其中 $\alpha_{ij} = \text{softmax}(Q_i \cdot K_j / \sqrt{d})$ 是注意力权重。

信息融合的原理：

  1. 选择性关注：权重 $\alpha_{ij}$ 大的时间点，其信息 $V_j$ 对输出的贡献大
  2. 信息聚合：所有时间点的信息都被考虑，但根据相关性加权
  3. 上下文感知：每个时间点的输出都融合了所有其他时间点的信息

实际例子：

假设我们要预测第60天（月底发薪日）的交易量：

  • 第1天（月底发薪日）：$V_1 = 50000$，权重 $\alpha_{60,1} = 0.35$
  • 第30天（月底发薪日）：$V_{30} = 48000$，权重 $\alpha_{60,30} = 0.35$
  • 第59天（前一天）：$V_{59} = 30000$，权重 $\alpha_{60,59} = 0.20$
  • 其他天：平均 $V_j = 25000$，总权重 $\sum \alpha_{60,j} = 0.10$

预测输出：
$$
\text{Output}_{60} = 0.35 \times 50000 + 0.35 \times 48000 + 0.20 \times 30000 + 0.10 \times 25000 = 42000
$$

模型自动识别出第1天和第30天都是月底发薪日，给它们分配高权重，从而预测第60天也会上涨。

完整的注意力公式

Scaled Dot-Product Attention：

$$
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V
$$

分步理解：

  1. 计算相似度：$Q K^T$ → 得到相似度矩阵
  2. 缩放：除以 $\sqrt{d_k}$ → 稳定训练
  3. 归一化：$\text{softmax}$ → 得到注意力权重（概率分布）
  4. 加权求和：权重 × $V$ → 融合信息

通俗理解：

  • Query是”问题”：我想了解什么？
  • Key是”索引”：哪些信息和我相关？
  • Value是”内容”：相关信息的具体内容
  • 通过相似度计算（Q×K^T）找到相关信息，通过softmax得到权重，最后加权求和（权重×V）得到答案

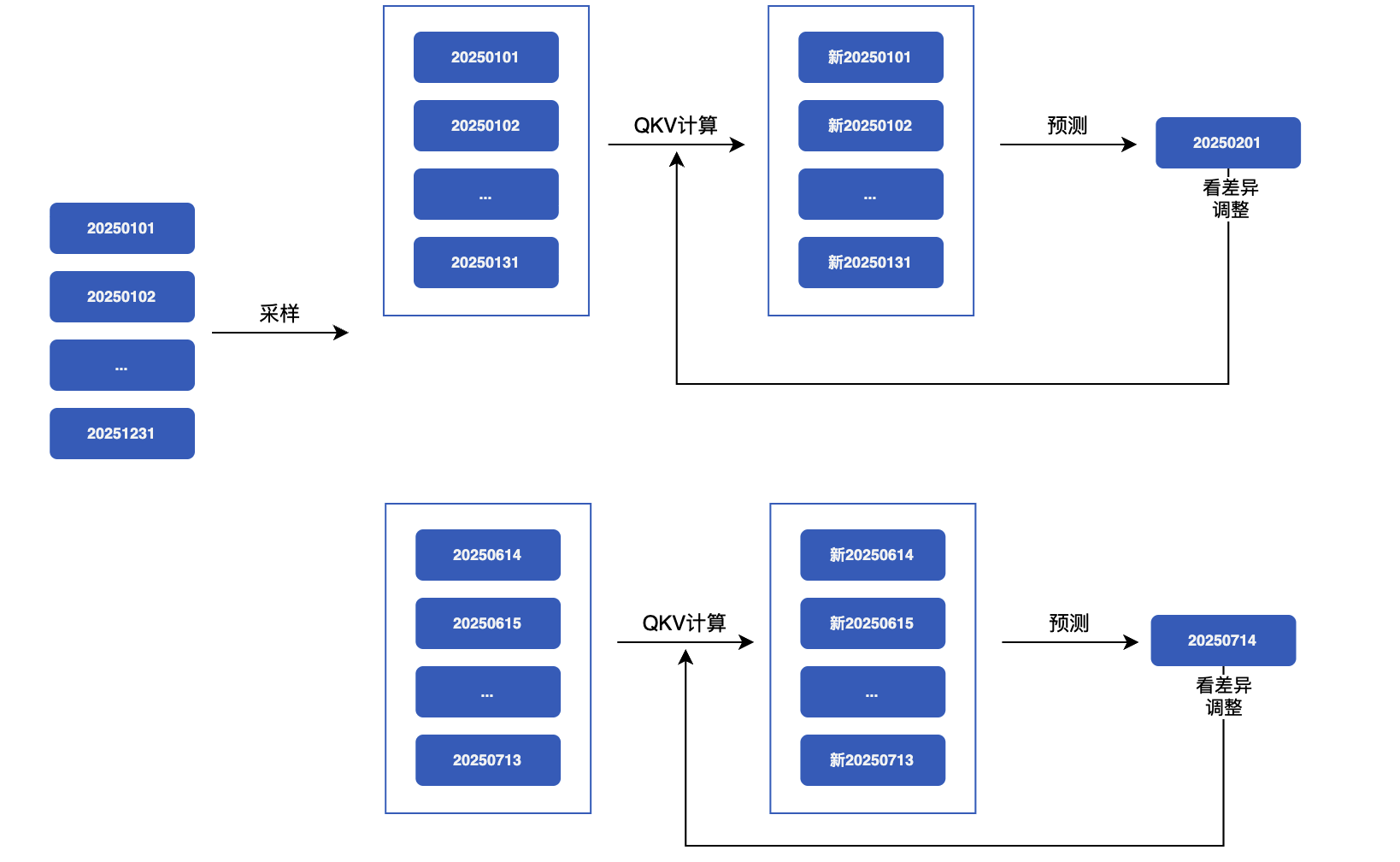
2.4 多头注意力机制

为什么需要多头？

就像人有多个感官（眼睛、耳朵、鼻子），每个感官关注不同的信息：

  • 眼睛关注视觉信息
  • 耳朵关注听觉信息
  • 鼻子关注嗅觉信息

多头注意力也是这个道理：

  • 头1：关注”周期性模式”（比如每月1号）
  • 头2：关注”趋势变化”（比如逐渐上涨）
  • 头3：关注”异常波动”（比如突然下跌）
  • 头4：关注”长期依赖”（比如30天前的模式）

每个头从不同角度理解时间序列，最后把所有信息融合起来。

graph TD
    A[输入序列] --> B[多头注意力]
    B --> B1[头1: 周期性]
    B --> B2[头2: 趋势]
    B --> B3[头3: 异常]
    B --> B4[头4: 长期依赖]
    B1 --> C[融合]
    B2 --> C
    B3 --> C
    B4 --> C
    C --> D[输出]
    
    style A fill:#e3f2fd
    style B fill:#fff3e0
    style B1 fill:#f3e5f5
    style B2 fill:#f3e5f5
    style B3 fill:#f3e5f5
    style B4 fill:#f3e5f5
    style C fill:#e8f5e9
    style D fill:#e1f5fe

2.5 Transformer的完整架构

原始Transformer架构：

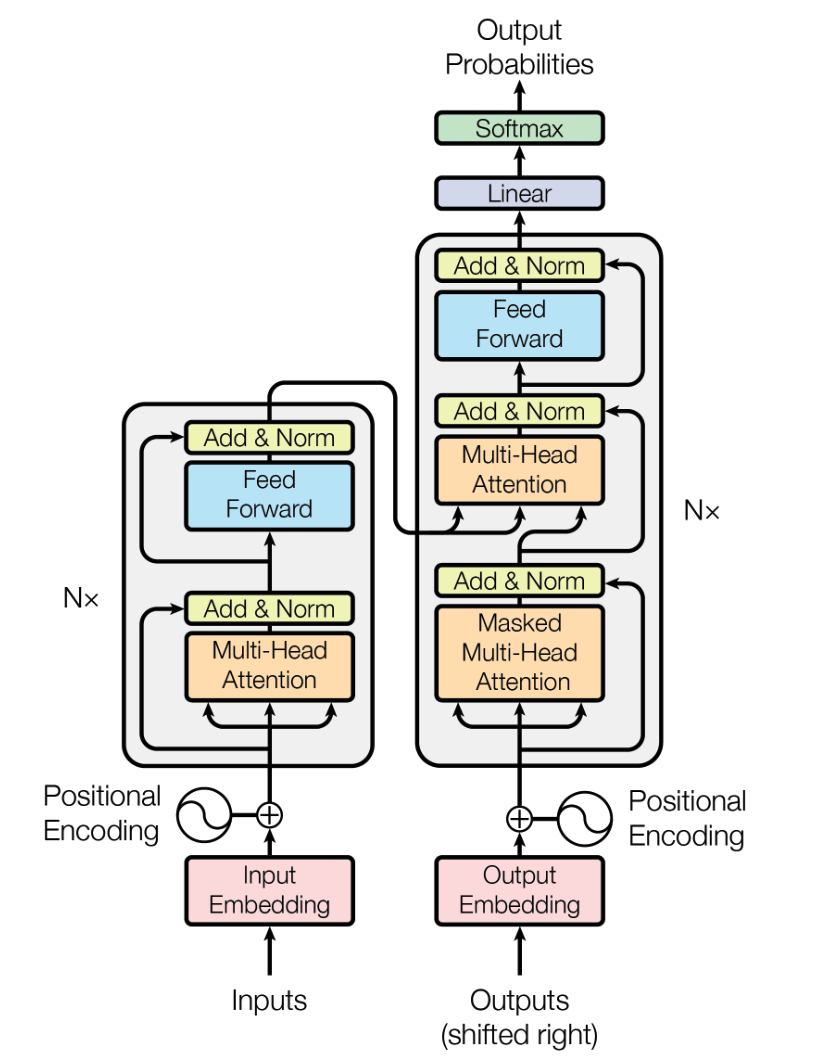
3 Timer的核心改进

3.1. 位置编码：时间位置信息的编码方式

为什么需要位置编码？

Transformer本身没有位置概念，需要告诉模型”这是第几个时间点”。

Timer使用位置编码：

  • 为每个token添加位置信息
  • 帮助模型理解时间顺序
  • 让模型知道”第1个token在时间上早于第2个token”

3.2 位置编码的数学公式

完整的位置编码公式：

对于位置 $pos$ 和维度 $i$，位置编码定义为：

$$
PE(pos, 2i) = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)
$$

$$
PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)
$$

其中：

  • $pos$：位置索引（第几个token，从0开始）
  • $i$：维度索引（$0 \leq i < d_{model}/2$）
  • $d_{model}$：模型维度（如1024）

3.3 为什么sin/cos能编码位置信息？

1. 唯一性：不同位置有不同的编码
2. 相对位置关系：可以表示位置差异

关键性质：

对于位置 $pos + k$，其编码可以表示为位置 $pos$ 和 $k$ 的编码的函数：

$$
PE(pos + k, 2i) = \sin\left(\frac{pos + k}{10000^{2i/d_{model}}}\right)
$$

$$
= \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\cos\left(\frac{k}{10000^{2i/d_{model}}}\right) + \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)\sin\left(\frac{k}{10000^{2i/d_{model}}}\right)
$$

$$
= PE(pos, 2i) \cdot PE(k, 2i+1) + PE(pos, 2i+1) \cdot PE(k, 2i)
$$

通俗理解：

  • 位置 $pos + k$ 的编码可以用位置 $pos$ 和偏移 $k$ 的编码组合得到
  • 这意味着模型可以学习”相对位置”关系
  • 例如：模型可以理解”第30天相对于第1天偏移了29天”

3.4 时序编码（TemporalEmbedding）的原理

为什么需要时序编码？

位置编码只告诉模型”这是第几个token”，但没有告诉模型”这是几点钟”、”这是星期几”、”这是几号”等时间信息。

时序编码的作用：

为每个时间点添加时间特征：

  • 小时（0-23）：一天中的哪个小时
  • 星期几（0-6）：一周中的哪一天
  • 日期（1-31）：一个月中的哪一天
  • 月份（1-12）：一年中的哪个月

输入数据格式（x_mark）：

时序编码的输入 x_mark 是一个形状为 [batch_size, seq_len, 5] 的张量，其中最后一个维度包含5个时间特征：

1
2
3
4
5
x_mark = [
    [月份, 日期, 星期几, 小时, 分钟],  # 第1个时间点
    [月份, 日期, 星期几, 小时, 分钟],  # 第2个时间点
    ...
]

示例：假设某个时间点是”2025年1月31日（星期五）下午3点”：

  • x_mark[0, 0, 0] = 1（1月）
  • x_mark[0, 0, 1] = 31（31号）
  • x_mark[0, 0, 2] = 4（星期五，0=周一，4=周五）
  • x_mark[0, 0, 3] = 15（15点，即下午3点）
  • x_mark[0, 0, 4] = 0（分钟，如果使用分钟级数据）

数学公式（类似位置编码）：

其中 c_in 是类别数（如24小时），d_model 是嵌入维度：

$$
\text{PE}{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d{model}}}\right)
$$

$$
\text{PE}{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d{model}}}\right)
$$

其中：

  • $pos \in {0, 1, 2, …, c_{in}-1}$：时间值的索引（如0-23表示小时）
  • $i \in {0, 1, 2, …, d_{model}/2-1}$：维度索引

示例：小时嵌入（24小时，d_model=1024）

对于”15点”（索引15）：

  • 第0维：$\text{PE}_{(15, 0)} = \sin(15 / 10000^{0/1024}) = \sin(15)$
  • 第1维：$\text{PE}_{(15, 1)} = \cos(15 / 10000^{0/1024}) = \cos(15)$
  • 第2维：$\text{PE}_{(15, 2)} = \sin(15 / 10000^{2/1024}) = \sin(15 / 10000^{0.00195})$
  • 第3维：$\text{PE}_{(15, 3)} = \cos(15 / 10000^{2/1024}) = \cos(15 / 10000^{0.00195})$
  • …
  • 第1022维：$\text{PE}_{(15, 1022)} = \sin(15 / 10000^{1022/1024})$
  • 第1023维：$\text{PE}_{(15, 1023)} = \cos(15 / 10000^{1022/1024})$

4 完整案例演示：从原始数据到预测结果

4.1 案例背景

业务场景：

  • 业务：PUBG（offerid=1450013788）
  • 渠道：谷歌钱包（gwallet）
  • 币种：USD
  • 目标：预测2025年2月1日的实时交易金额（amt_cny_realtime）

输入数据：

  • 时间范围：2025年1月1日到2025年1月31日（31天，744小时）
  • 数据格式：每小时一条记录
  • 数据维度：17个特征（包括目标变量和其他统计特征）

示例原始数据：

1
2
3
4
5
6
statis_hour,offerid,fpay_chan,currencytype,amt_cny_realtime,amt_cny_realtime_last7day,...
20250101,1450013788,gwallet,USD,48658,16798,...
20250102,1450013788,gwallet,USD,47658,15798,...
20250103,1450013788,gwallet,USD,46520,15234,...
...
20250131,1450013788,gwallet,USD,36710,13272,...

数据特点：

  • 每天24小时，共31天 = 744小时的数据
  • 每个时间点包含17个特征
  • 目标变量：amt_cny_realtime（实时交易金额）

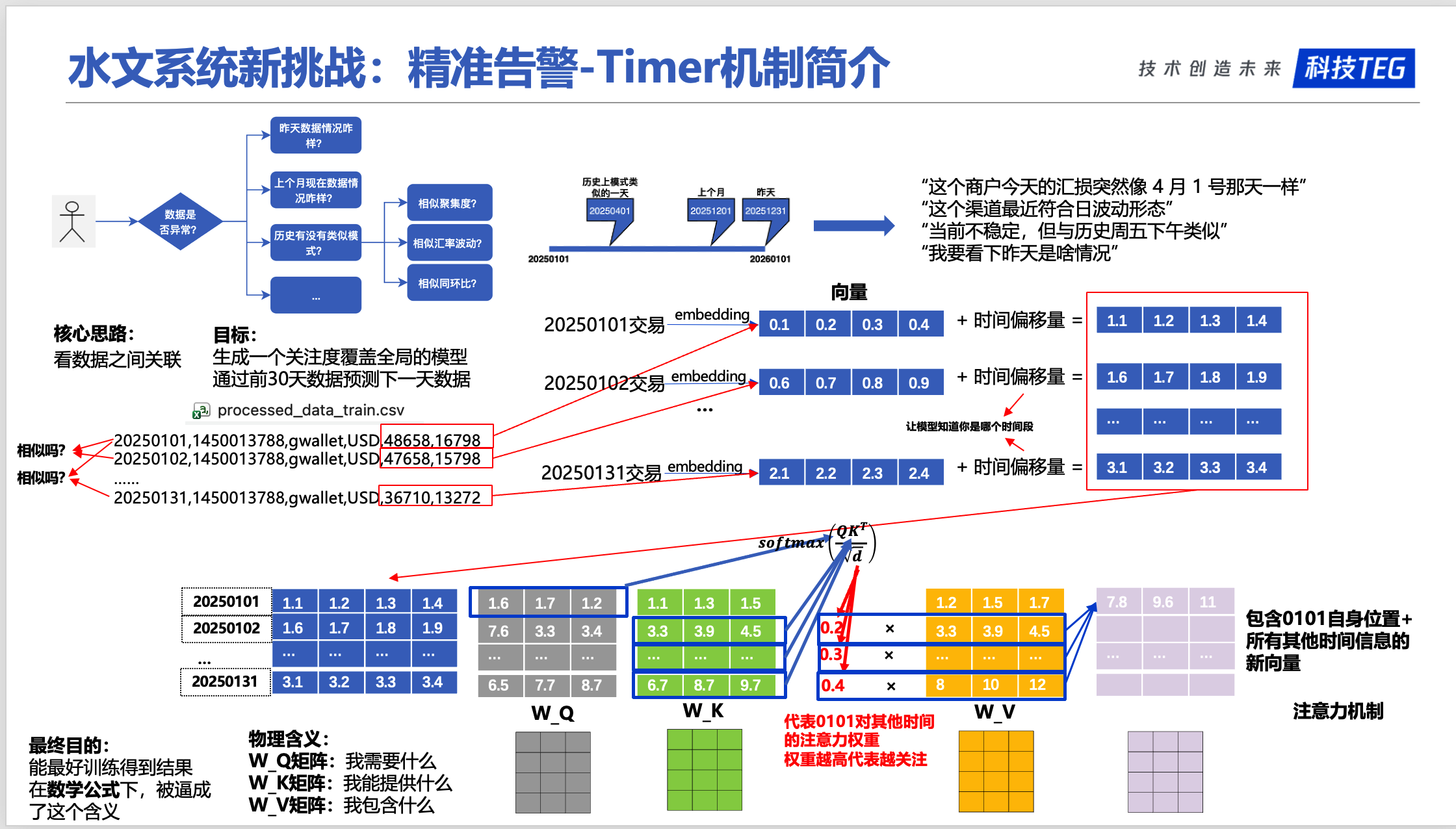
Timer Token化和QKV机制

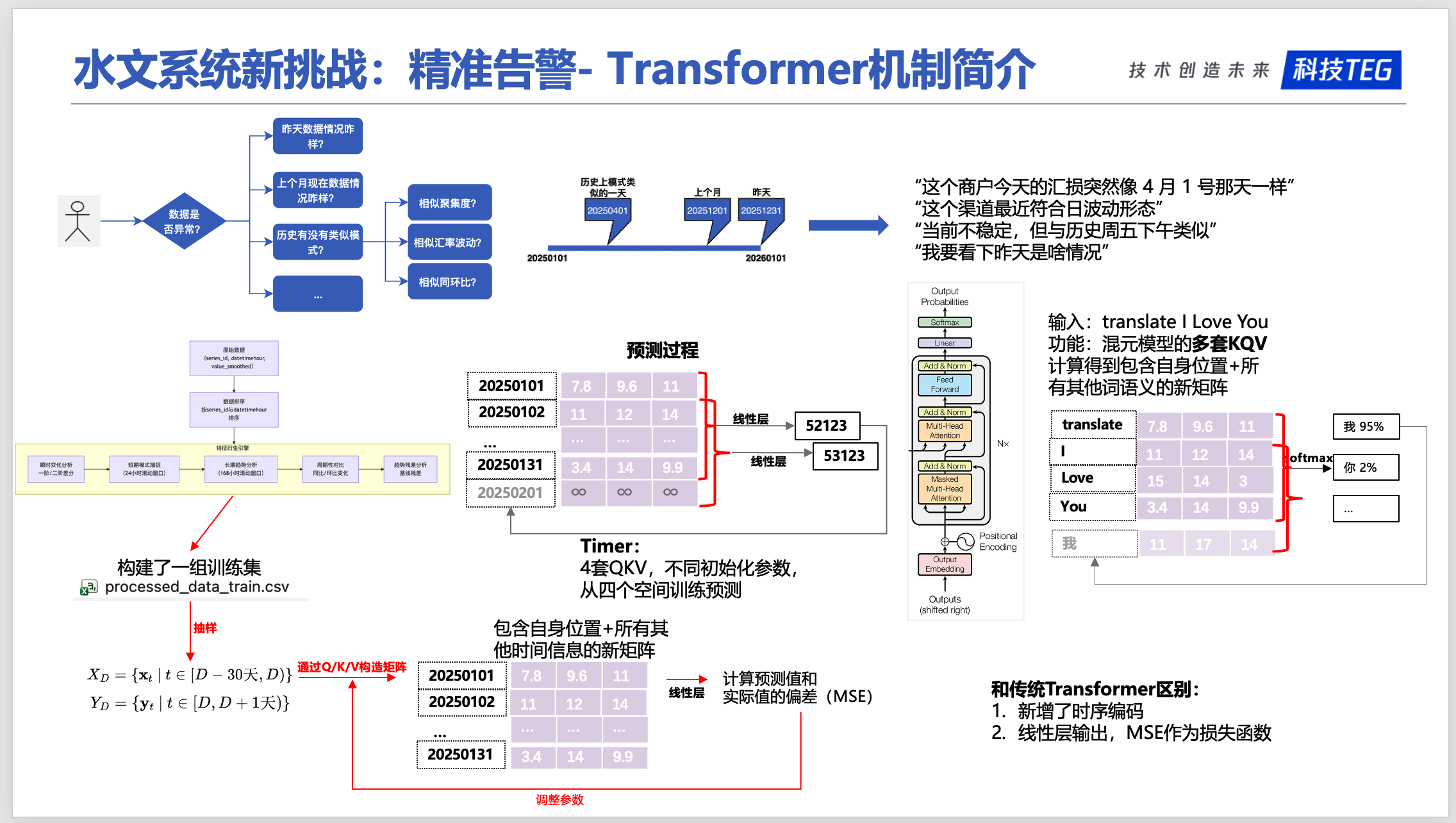
Timer数据预处理和特征工程

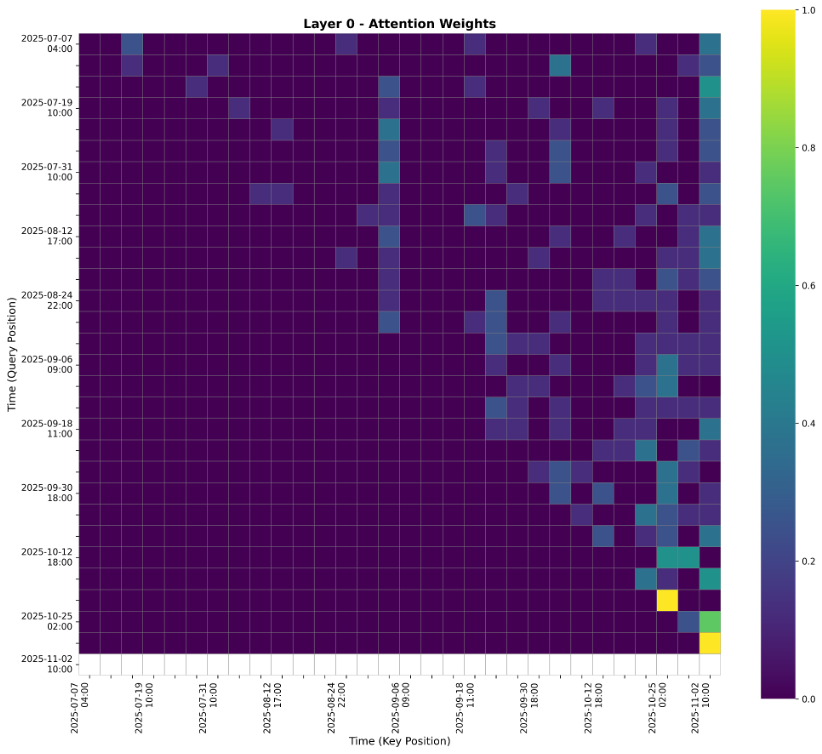
4.2 预测效果可视化

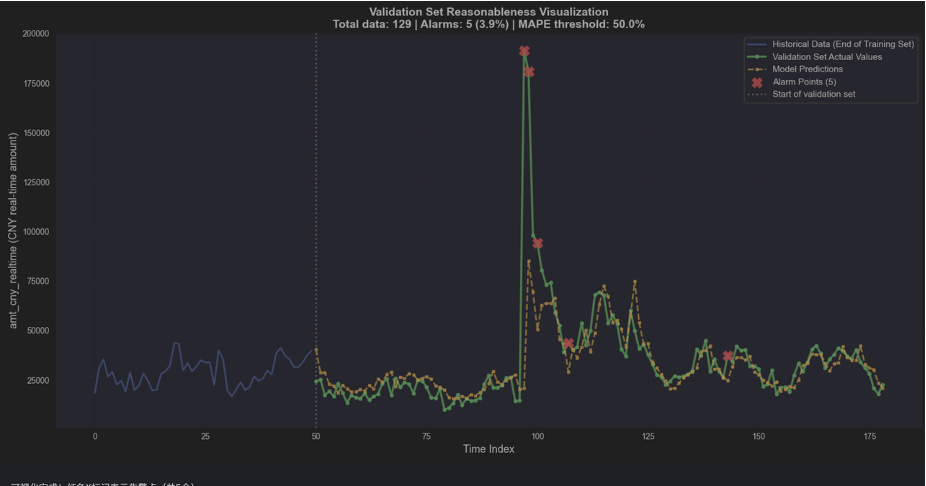
预测效果可视化

4.3 注意力权重可视化

注意力权重可视化

AI > Attention
http://example.com/2024/01/1ea79973cb1d.html
作者
CoachHe
发布于
2024年1月18日
许可协议